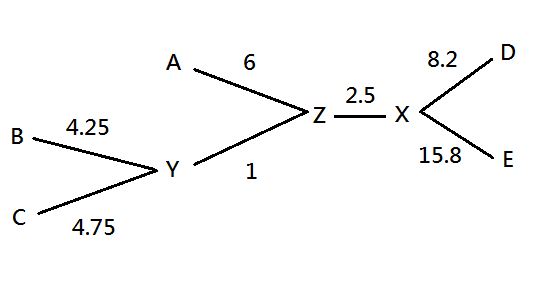Neighbor Joining (phylogeny tree)

  • Saitou et al. (1987) The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol Biol Evol 4(4), 406-425

Several tree construction methods

distance-based character-based
similar with character-based more reliable, more biological
fast, simple slower, complex
the number of nucleotide/ amino acid differences Interpret molecular changes in the context (shared derived characters)
much popular -
  • Neighbor-joining
    1. a clustering method
    2. distance-based method
    3. the principle is minimal evolution : the building tree preferred with the smallest branch length in each step

Example : Molecular phylogeny

  • a science: DNA, RNA & protein sequences used to deduce(trace) relationships

  • relationships are like :

  • distance matrix example
# molecular sequence example
> seqA 
ATCGATCG 
> seqB 
ATCCATCG 
> seqC 
ATCATTCC
seqA seqB seqC
seqA 0 1 3
seqB 1 0 3
seqC 3 3 0
  • Used example : initial distance matrix 
# sequence alignment 
A: gorilla 
B: chimpanzee 
C: human 
D: orangutan 
E: macaque
B C D E
A 11 12 17 24
B 9 16 24
C 16 24
D 24

STEP 1 (N = 5 nodes remained)

  • calculate $$Sx value = \sum^{N}{i=1}{d_{xi}}$$，N = operation taxonomic units

    1. $$SA = S{AB} + S{AC} + S{AD} + S_{AE} = 11 + 12 + 17 + 24 = 64$$
    2. $$SB = S{BA} + S{BC} + S{BD} + S_{BE} = 11 + 9 + 16 + 24 = 60$$
    3. $$S_C = 61$$
    4. $$S_D = 73$$
    5. $$S_E = 96$$

  • calculate $$\beta{ij} = d{ij}-\frac{S_i + S_j}{N-2}$$

    1. $$\beta_{AB} = 11 - \frac{64 + 60}{5 - 2} = -30.3$$
    2. $$\beta_{AC} = 12 - \frac{64+61}{5-2} = -29.7$$
    3. $$\beta_{AD} = 17 - \frac{64 + 73}{5-2} = -28.7$$
    4. calculate all $$\beta{ij}$$ ($$\beta{ij}$$ joined as neighbors)

  • New matrix: related total branch length

B C D E
A -30.3 -29.7 -28.7 -29.3
B -29.7 -28.3 -28
C -28.7 -28.3
D -32.3
  • Construct a tree : the smallest total branch length: added to the previous tree built

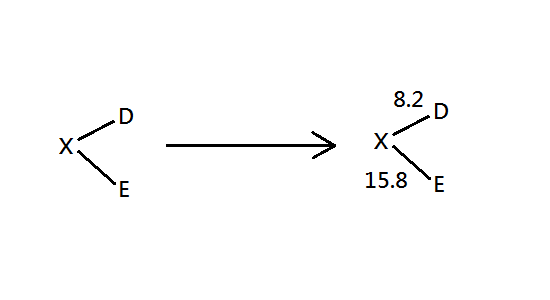
  • new node (X): combine node D and node E
    1. $$d{DX}=[d{DE} + \frac{S_D-S_E}{N-2}] / 2 = [24 + \frac{73-96}{3}] / 2 = 8.2$$
    2. $$d{EX} = d{DE}-d_{DX} = 24-8.2 = 15.8$$

STEP 2 (N = 4 nodes remained)

  • calculate new $$d_{ij}$$ value

    1. $$d{XA} = (d{DA} + d{EA} - d{DE}) / 2 = (17 + 24 - 24) / 2 = 8.5$$
    2. $$d{XB} = (d{DB} + d{EB} - d{DE}) / 2 = (16 + 24 -24)/2 = 8$$
    3. $$d{XC} = (d{DC} + d{EC} - d{DE}) / 2 = 8$$

  • new distance matrix: x represents both node D and node E

B C X
A 11 12 8.5
B 9 8
C 8

  • calculate $$Sx value = \sum^{N}{i=1}{d_{xi}}$$，N = operation taxonomic units

    1. $$SA = S{AB} + S{AC} + S{AX} = 11 + 12 + 8.5 = 31.5$$
    2. $$SB = S{BA} + S{BC} + S{BX} = 11 + 9 + 8 = 28$$
    3. $$SC = S{CA} + S{CB} + S{CX} = 12 + 9 + 8 = 29$$
    4. $$SX = S{XA} + S{XB} + S{XC} = 8.5 + 8 + 8 = 24.5$$

  • calculate $$\beta{ij} = d{ij}-\frac{S_i + S_j}{N-2}$$

    1. $$\beta_{AB} = 11-(31.5+28)/2 = -18.75$$
    2. $$\beta_{AC} = 12 - (31.5+29)/2 = -18.25$$
    3. calculate all $$\beta_{ij}$$

  • New matrix: related total branch length

B C X
A -18.75 -18.25 -19.5
B -19.5 -18.25
C -18.75
  • Construct a tree : the smallest total branch length: added to the previous tree built

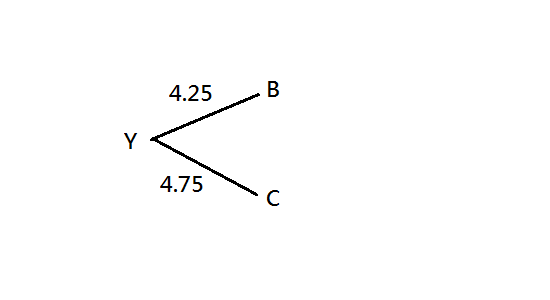
  • new node (Y): combine node B and node C
    1. $$d{BY} = [d{BC} + \frac{S_B - S_C}{N-2}]/2 = [9 + \frac{28-29}{2}]/2=4.25$$
    2. $$d{CY} = d{BC} - d_{BY} = 9 - 4.25 =4.75$$

STEP 3 (N = 3 nodes remained)

  • new distance matrix

    1. X represents both node D and node E
    2. Y represents both node B and node C
    3. $$d{YA} = (d{BA} + d{CA} - d{BC}) / 2 = (11 + 12 - 9) / 2 = 7$$
    4. $$d{YX} = (d{BX} + d{CX} -d{BC})/2 = (8 + 8 - 9)/2=3.5$$

  • new distance matrix: Y represents both node B and node C

Y X
A 7 8.5
Y 3.5

  • calculate $$Sx value = \sum^{N}{i=1}{d_{xi}}$$，N = operation taxonomic units

    1. $$SA = S{AX} + S_{AY} = 8.5 + 7 = 15.5$$
    2. $$SX = S{XA} + S_{XY} = 8.5 + 3.5 = 12$$
    3. $$SY = S{YA} + S_{YX} = 7 + 3.5 = 10.5$$

  • calculate $$\beta{ij} = d{ij}-\frac{S_i + S_j}{N-2}$$

    1. $$\beta_{AY} = 7 – (15.5 + 10.5)/1 = -19 $$
    2. $$\beta_{AX} = 8.5 – (15.5 + 12)/1 = -19 $$
    3. $$\beta_{XY} = 3.5 – (12 + 10.5)/1 = -19$$

  • New matrix: related total branch length

Y X
A -19 -19
Y -19

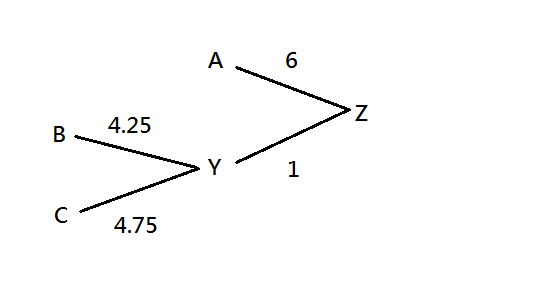
  • new node (Z): combine node A and node Y

    1. $$d{AZ} = [d{AY} + \frac{S_A - S_Y}{N-2}]/2 = [7 + \frac{15.5-10.5}{1}]/2 = 6$$
    2. $$d{YZ} = d{AY} - d_{AZ} = 7 -6 = 1$$

  • Construct a tree : the smallest total branch length: added to the previous tree built

STEP 4 (N = 2 nodes remained)

  • new distance matrix:

    1. X represents both node D and node E
    2. Y represents both node B and node C
    3. Z represents both node A and node Y
    4. $$d{XZ} = (d{AX} + d{YX} - d{AY})/2 = (8.5+3.5-7)/2=2.5$$

  • new distance matrix : Z represents both node A and node Y

X
Z 2.5

  • calculate $$Sx value = \sum^{N}{i=1}{d_{xi}}$$，N = operation taxonomic units

    1. $$SX = S{XZ} = 2.5 = S_{XZ} = S_Z$$

  • Construct a tree : the smallest total branch length: added to the previous tree built

results matching ""

    No results matching ""